리스크 패리티(Risk Parity)와 손해율
0. 들어가며
- 하기에 서술된 모든 내용은 이전에 개발한 가상 언더라이팅(Virtual Underwriting)의 경우와 마찬가지로 개인적으로 생각해 왔던 여러 아이디어의 실험 과정 중 하나로 이해해주길 바란다.
- 데이터는 Yahoo!finance의 주가 데이터와 실제 질병수술담보 손해율에 기반한 가상의 데이터, 도구는 개인적으로 개발한 패키지를 활용하였다.
1. 리스크 패리티(Risk Parity)란?
- 리스크 패리티(Risk Parity)는 각 자산이 포트폴리오 전체 변동성에 동일한 기여를 하도록 구성된 투자 전략이다. 이는 전통적인 자산 배분 전략(Mean-Variance Optimization, 60/40 포트폴리오 등)과 달리, 각 자산군의 리스크 기여도를 균형적으로 조정하여 분산 투자의 효과를 극대화하는 데 초점을 맞춘다.
2. 리스크 패리티의 핵심 개념
1) 자산별 리스크 기여도(Equal Risk Contribution)
- 각 자산의 변동성이 다르므로, 단순히 투자 비율을 맞추는 것이 아니라 각 자산이 전체 포트폴리오 변동성에 동일한 영향을 미치도록 가중치를 조정해야 한다.
- 이를 위해 자산별 리스크 기여도(Risk Contribution, RC)를 계산한다.
2) 리스크 패리티 공식
- Risk Parity 포트폴리오에서는 각 자산 \(i\) 의 리스크 기여도(Contribution to Risk, \(CR_i\))가 동일해야 한다.
a. 포트폴리오 전체 리스크 (\(\sigma_p\))
\[ \sigma_p = \sqrt{ w^T \Sigma w } \] * \(w\) : 포트폴리오 가중치 벡터 (\(n \times 1\)) - \(\Sigma\) : 공분산 행렬 (\(n \times n\))
b. 각 자산의 Marginal Risk Contribution (MRC)
\[ MRC_i = \frac{\partial \sigma_p}{\partial w_i} = \frac{(\Sigma w)_i}{\sigma_p} \]
c. 각 자산의 Total Risk Contribution (TRC)
\[ TRC_i = w_i MRC_i = w_i \frac{(\Sigma w)_i}{\sigma_p} \]
- 모든 자산의 TRC가 동일하도록 \(TRC_1 = TRC_2 = ... = TRC_n\)을 만족시키는 \(w\) 를 구하는 것이 목표이다.
3) 예제
- 주식(Equity), 채권(Bond), 금(Gold), 부동산(Real Estate) 자산 등으로 구성된 포트폴리오 (2007.07 ~ 2025.03)를 만들어 보자.
--------|--------------------------------------------------------------------
Ticker | Name
--------|--------------------------------------------------------------------
SPY | SPDR S&P 500 ETF Trust (미국 S&P 500)
VEA | Vanguard FTSE Developed Markets Index Fund ETF Shares (선진국 주식)
VWO | Vanguard Emerging Markets Stock Index Fund (개도국 주식)
IEF | iShares 7-10 Year Treasury Bond ETF (중기채)
TLT | iShares 20+ Year Treasury Bond ETF (장기채)
GLD | SPDR Gold Shares (금)
VNQ | Vanguard Real Estate Index Fund ETF Shares (부동산)
--------|--------------------------------------------------------------------논의를 간단히 하기위해 각 자산을 1/n의 비율로 동일하게 배분하면,
하기 포트폴리오의 연평균 성장률(Compound Average Growth Rate)은 6.5%, 최대 낙폭(Maximum Drawdown)은 39.2%를 보여준다. 동일비중 포트폴리오만으로도 변동성을 꽤 준수하게 낮출 수 있다.
비중 최적화와 관계없이 자산 배분 그 자체만으로도 포트폴리오 수익률 곡선을 개별 자산의 수익률 곡선보다 부드럽게 만들어 주고(변동성 감소), 최대낙폭도 개선해 주는 것을 확인할 수 있다.
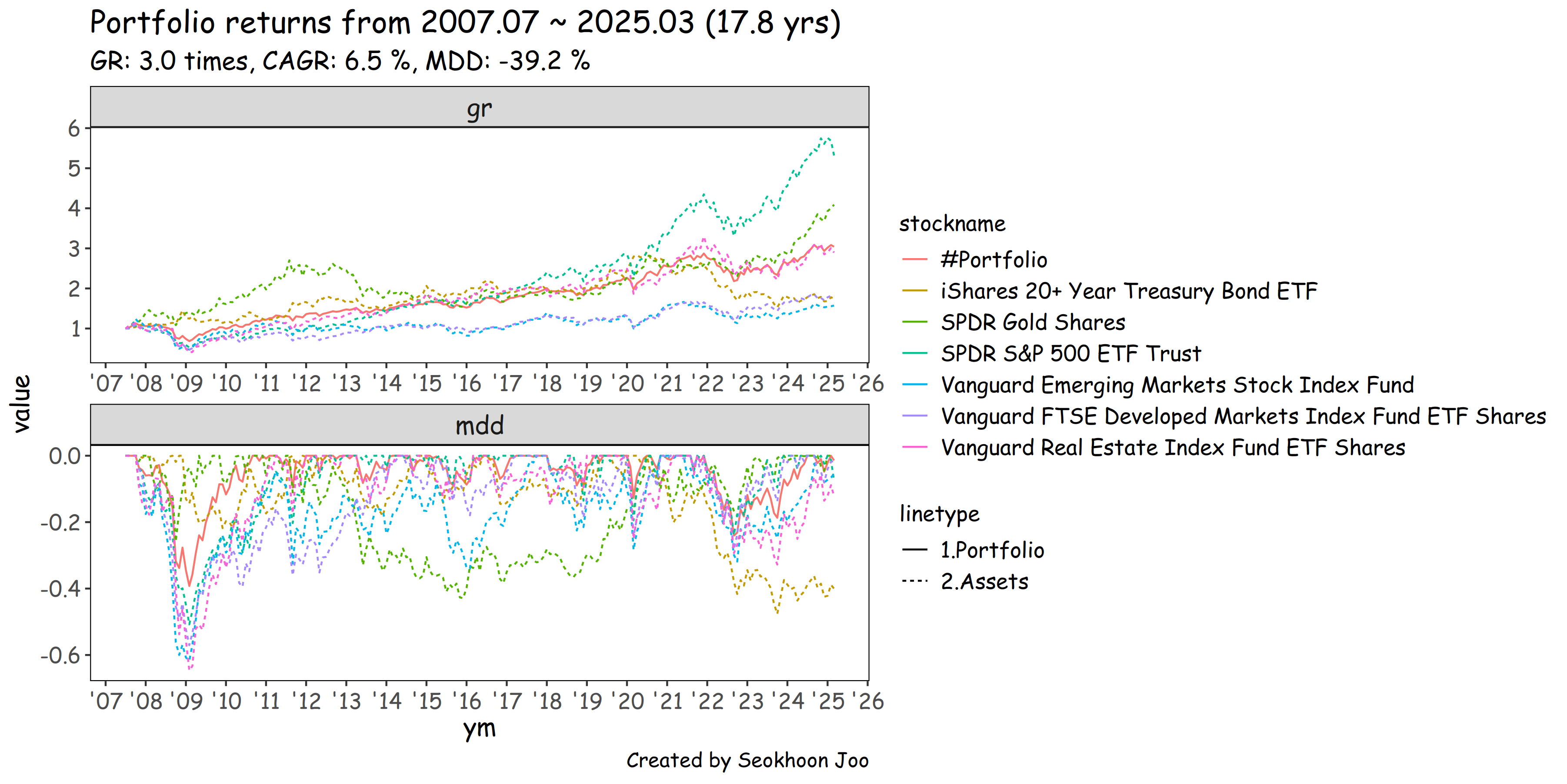
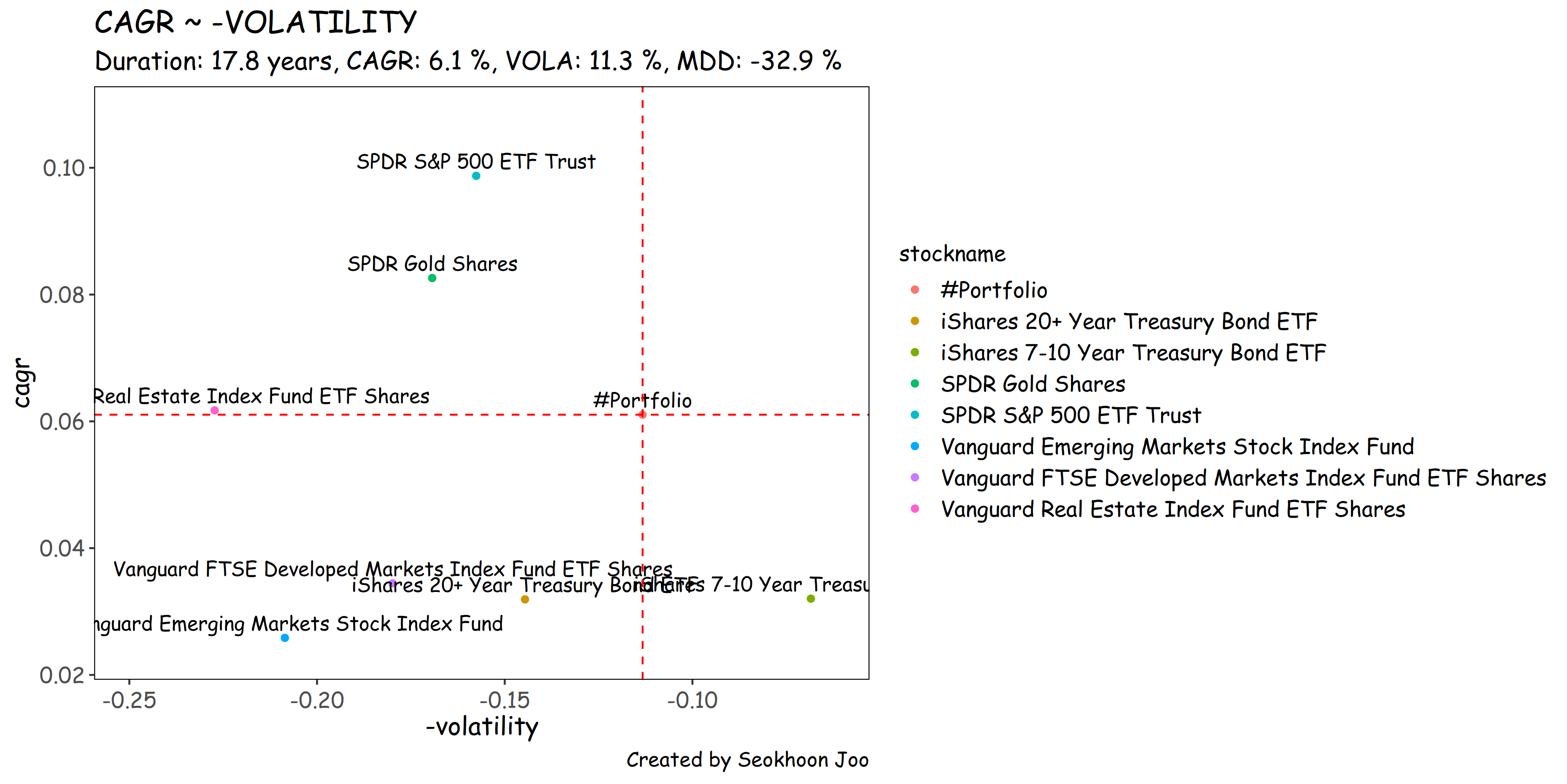
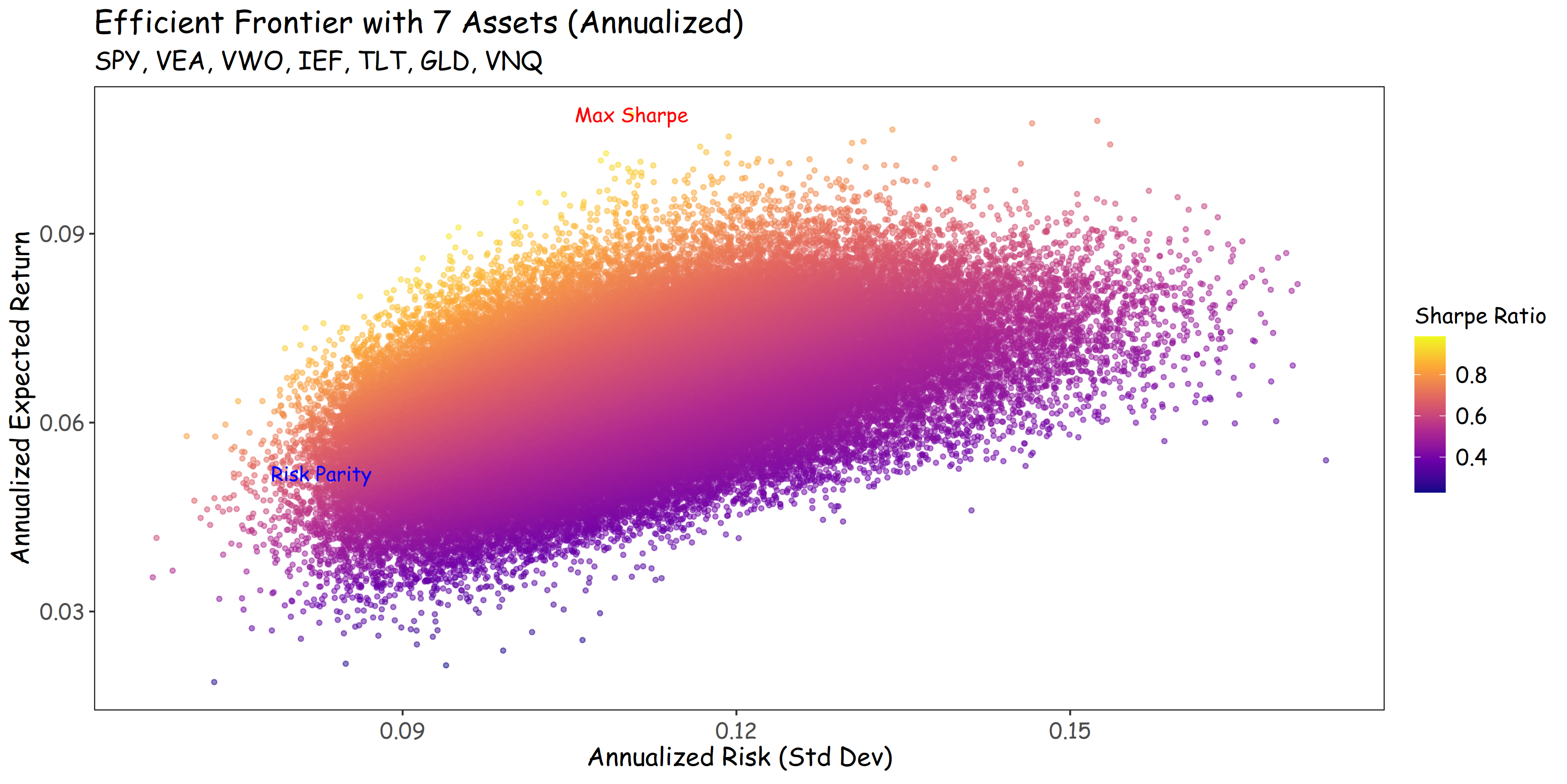
- 연평균수익률(CAGR)과 변동성(Volatility)의 그래프에서 포트폴리오는 적절한 그 어디쯤을 차지하는 것을 알 수 있다.
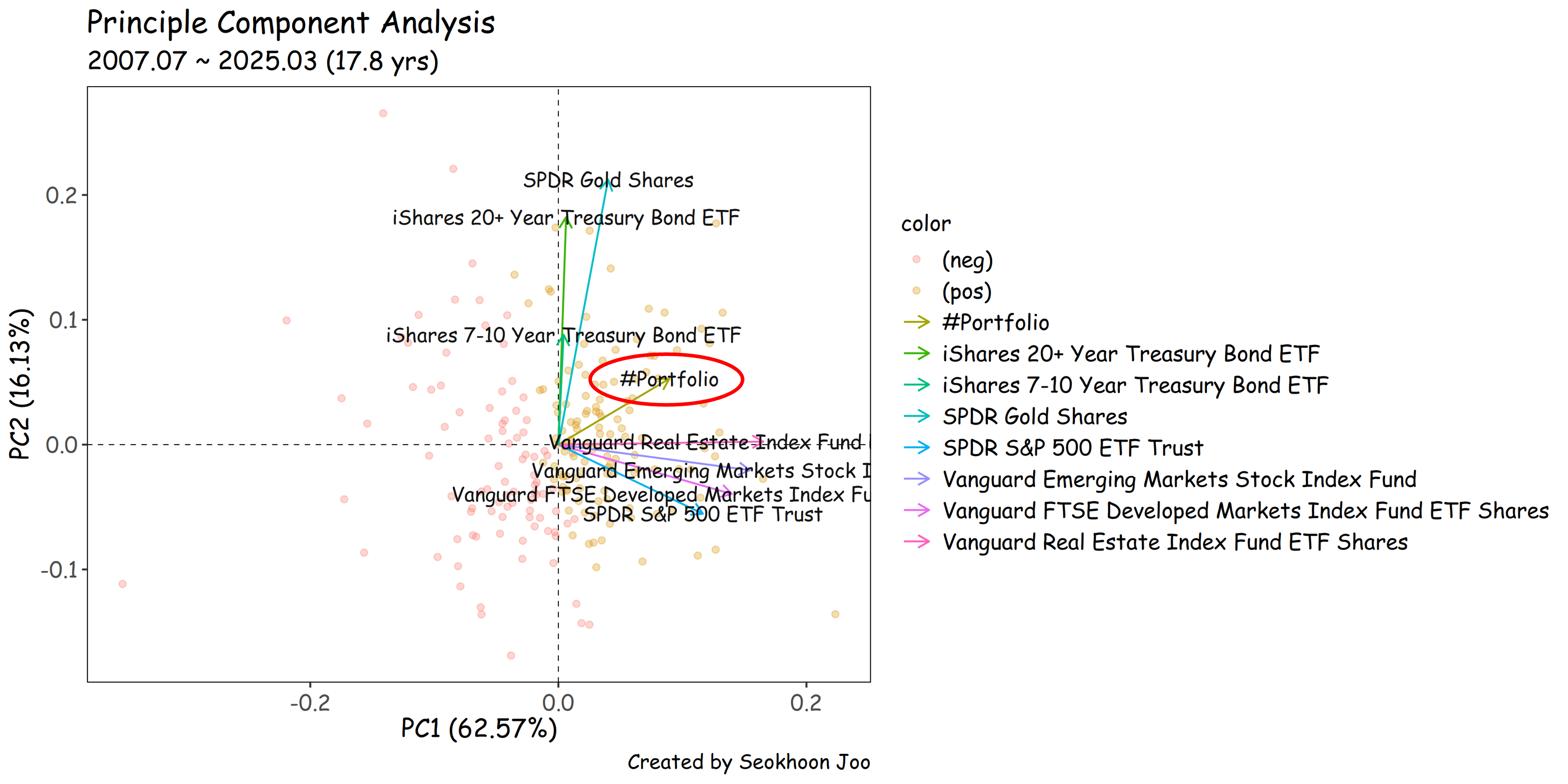
PCA (Principal Component Analysis) 분석을 통해 각 자산군의 수익률 상관관계를 2차원 공간에 투영하면 각 자산이 서로 다른 방향으로 부드럽게 흩어져 있는 것을 알 수 있다. (적절한 자산배분)
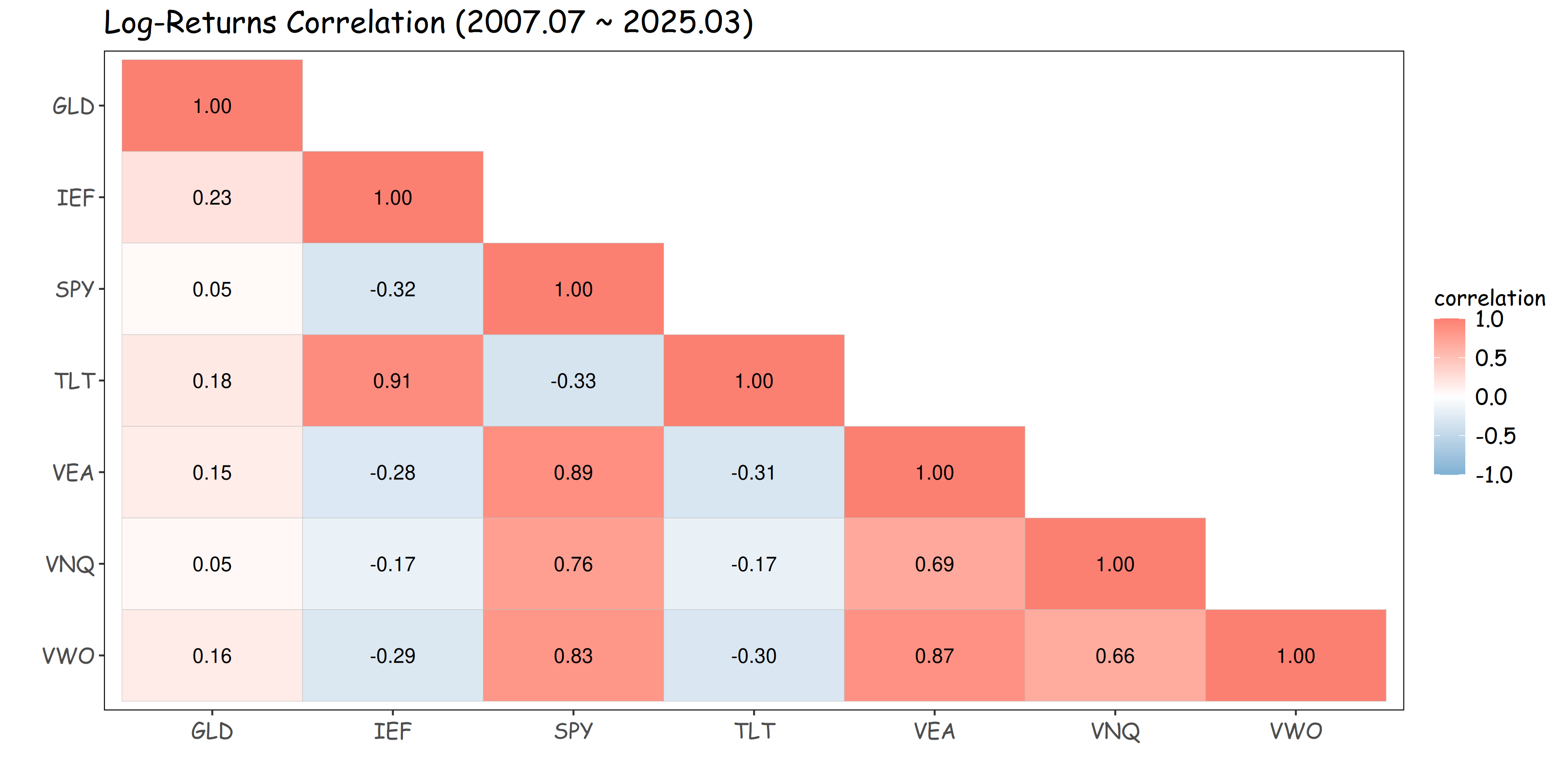
다음 수익률의 상관관계를 통해 리스크 패리티 포트폴리오를 구하게 된다.
각 자산군의 비중에 따른 위험-수익 그래프상에서 Risk Parity는 다음과 같은 위치에 있게 된다.
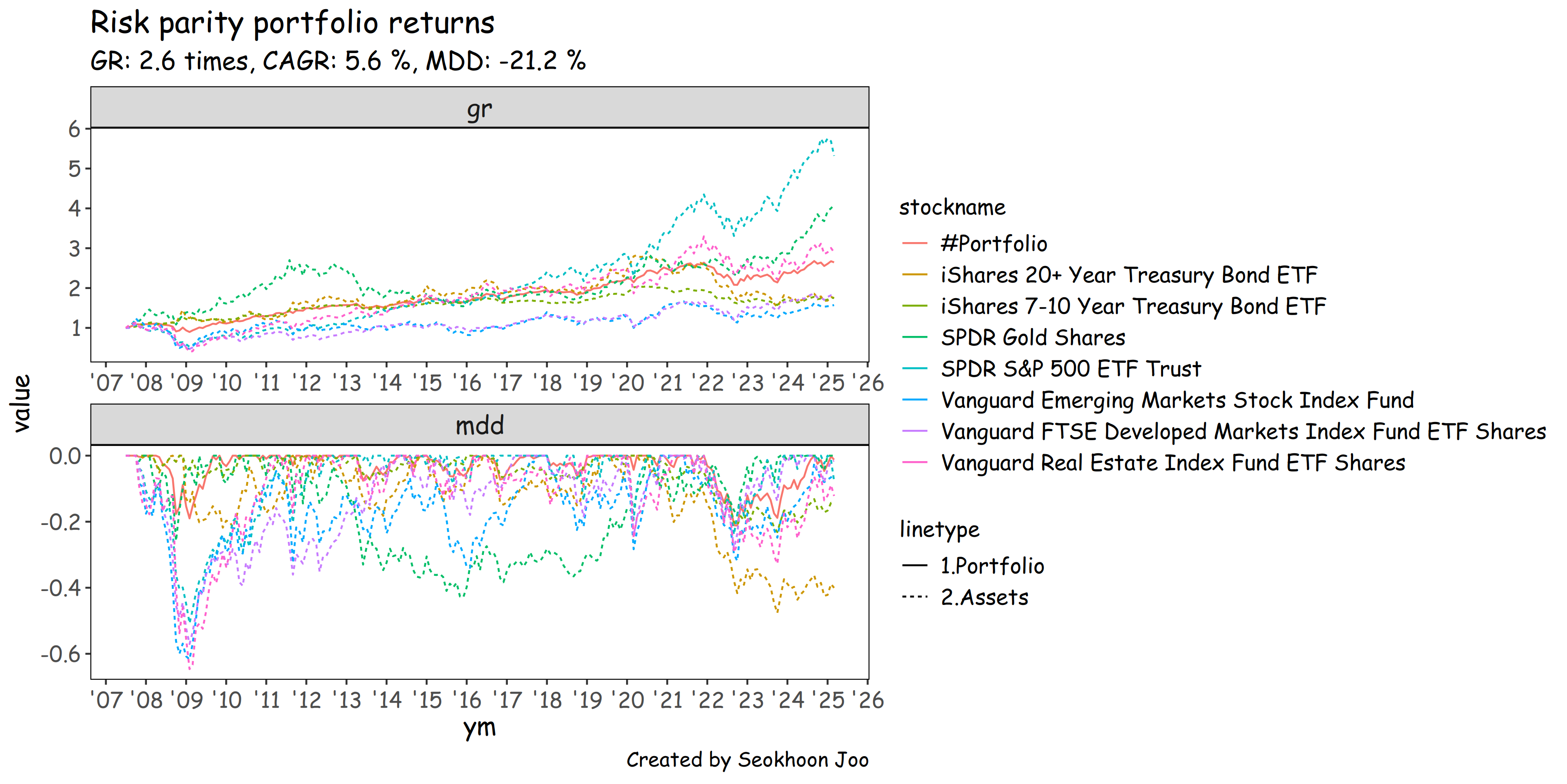
리스크 패리티 포트폴리오의 성과
--------|-------------------------|--------|--------|-------|--------|-------
Ticker | Name | Weight | Parity | Cagr | Mdd | Vola
--------|-------------------------|--------|--------|-------|--------|-------
| Portfolio | 1.000 | 1.000 | 0.061 | -0.329 | 0.113
--------|-------------------------|--------|--------|-------|--------|-------
SPY | S&P 500 | 0.143 | 0.120 | 0.099 | -0.508 | 0.158
VEA | Developed Markets | 0.143 | 0.096 | 0.034 | -0.571 | 0.180
VWO | Emerging Markets | 0.143 | 0.088 | 0.026 | -0.617 | 0.209
IEF | 7-10 Year Treasury Bond | 0.143 | 0.322 | 0.032 | -0.232 | 0.068
TLT | 20+ Year Treasury Bond | 0.143 | 0.162 | 0.032 | -0.476 | 0.145
GLD | Gold | 0.143 | 0.136 | 0.083 | -0.429 | 0.169
VNQ | Real Estate | 0.143 | 0.076 | 0.062 | -0.646 | 0.227
--------|-------------------------|--------|--------|-------|--------|-------- 주식과 채권의 변동성 차이가 크기 때문에, 동일비중으로 투자할 경우 포트폴리오의 변동성은 주식이 중심이 된다. (Weight 컬럼)
- 리스크 패리티를 적용하면 변동성이 작은 채권이 더 큰 역할을 하도록 배분되는 결과가 도출된다. (Parity 컬럼)
- 이는 시장 상황에 흔들리지 않고 더 안정적인 성과를 기대할 수 있도록 설계된 전략이다.
- 다만 Risk-return trade-off에 따라 수익률이 하락한다.
- 변동성이 낮은 채권이 높은 가중치를 받으므로 금리 상승기에 성과가 악화될 가능성이 있다. (코로나 이후 금리 상승기, TLT와 같은 장기국채의 수익률이 최대 -48.4%, EDV같은 제로쿠폰 장기국채는 -60.0% 까지 하락했다.)
3. 손해율 리스크 패리티
1) 적용
다양한 자산을 조합하여 포트폴리오를 구성하듯이, 보험에서도 상품, 담보, 고객 등의 분류를 통해 판매 목표를 조절할 수 있다. 이러한 분류를 적절히 활용하면 리스크를 효과적으로 관리하고, 보다 안정적인 손익 구조를 구축할 수 있다.
투자에서는 변동성이 비교적 명확하게 정의되지만, 손해율에서의 변동성은 해석이 모호할 수 있다. 가입한도, 판매 건수, 위험보험료(면책 및 감액 조건 포함), 클레임 발생률 등 다양한 요소가 손해율의 변동성에 영향을 미칠 수 있으며, 이를 어떻게 정의하느냐에 따라 분석 결과가 달라질 수 있으므로 이를 분석하는 데 충분한 시간을 할애해야 한다.
여기서는 논의를 간단히 하기 위해 질병수술 담보의 25회차 누적 손해율이 확인 가능한 UY월도(12개 월도)의 평균 및 표준편차를 리스크 패리티의 수익률과 변동성으로 정의하였다.
2) 예제 (고객 연령군 판매비중 목표 설정)
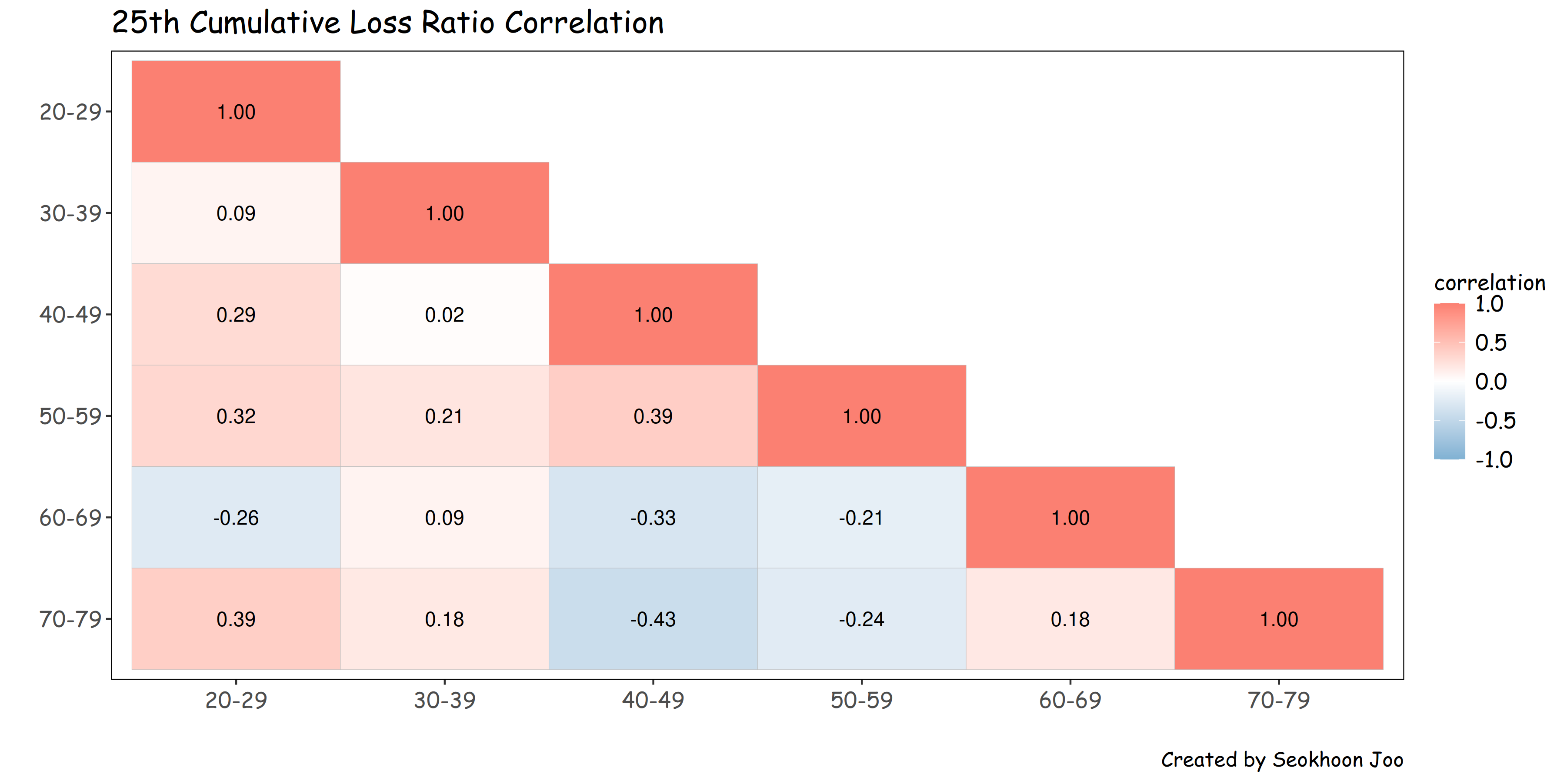
다음은 연령군별 25회차 누적 손해율을 심사월별로 표기한 것이다. (예를 들어 30대의 25년 1월의 25회차 손해율, 25년 2월의 25회차 손해율, …, 25년 12월의 25회차 손해율)
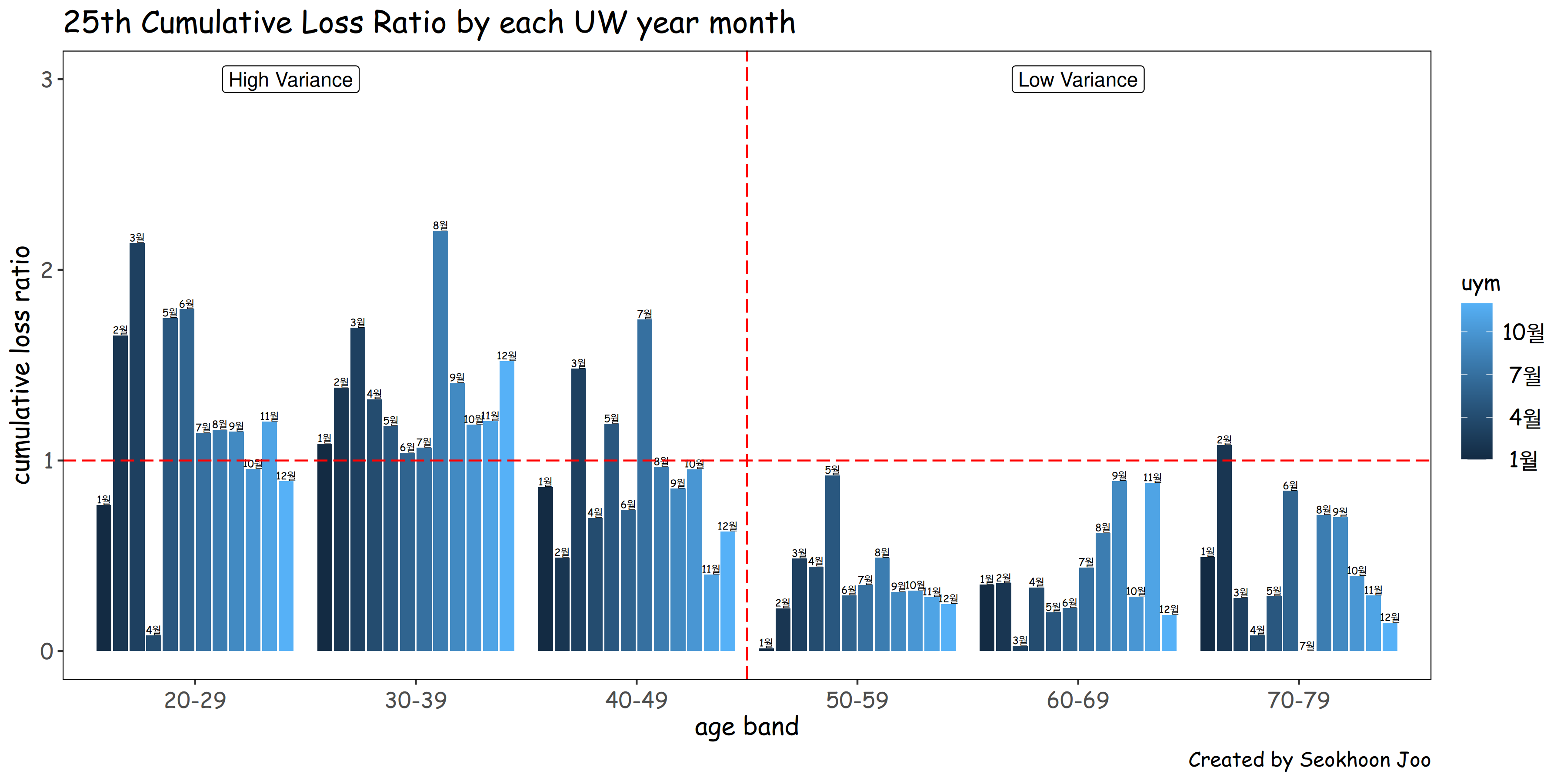
독립 가정 등을 평가하기 위해 PCA 분석과 상관관계 분석을 동시에 수행해 보았다.
PCA (Principal Component Analysis) 분석
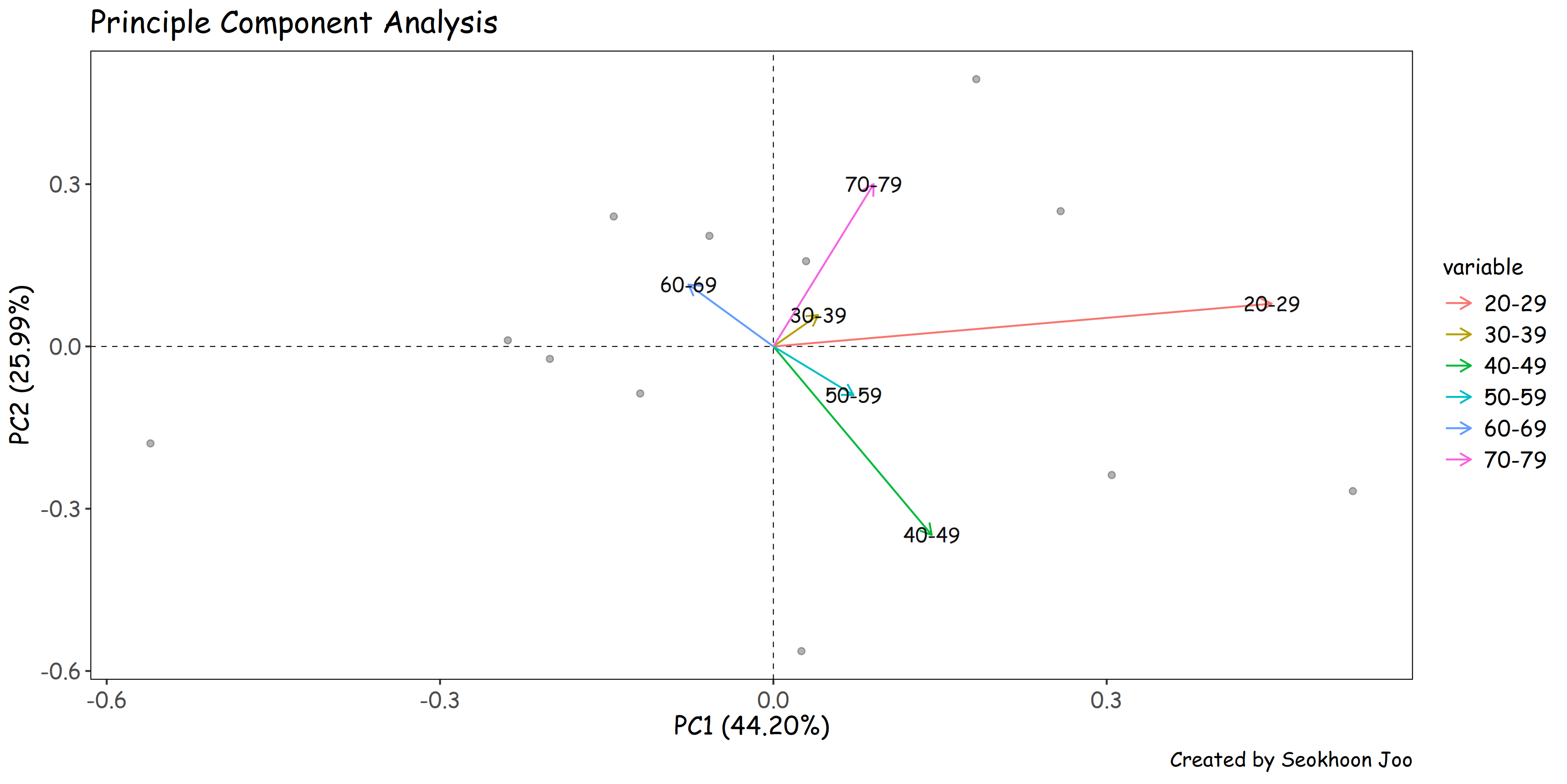
연령군과 손해율의 상관관계
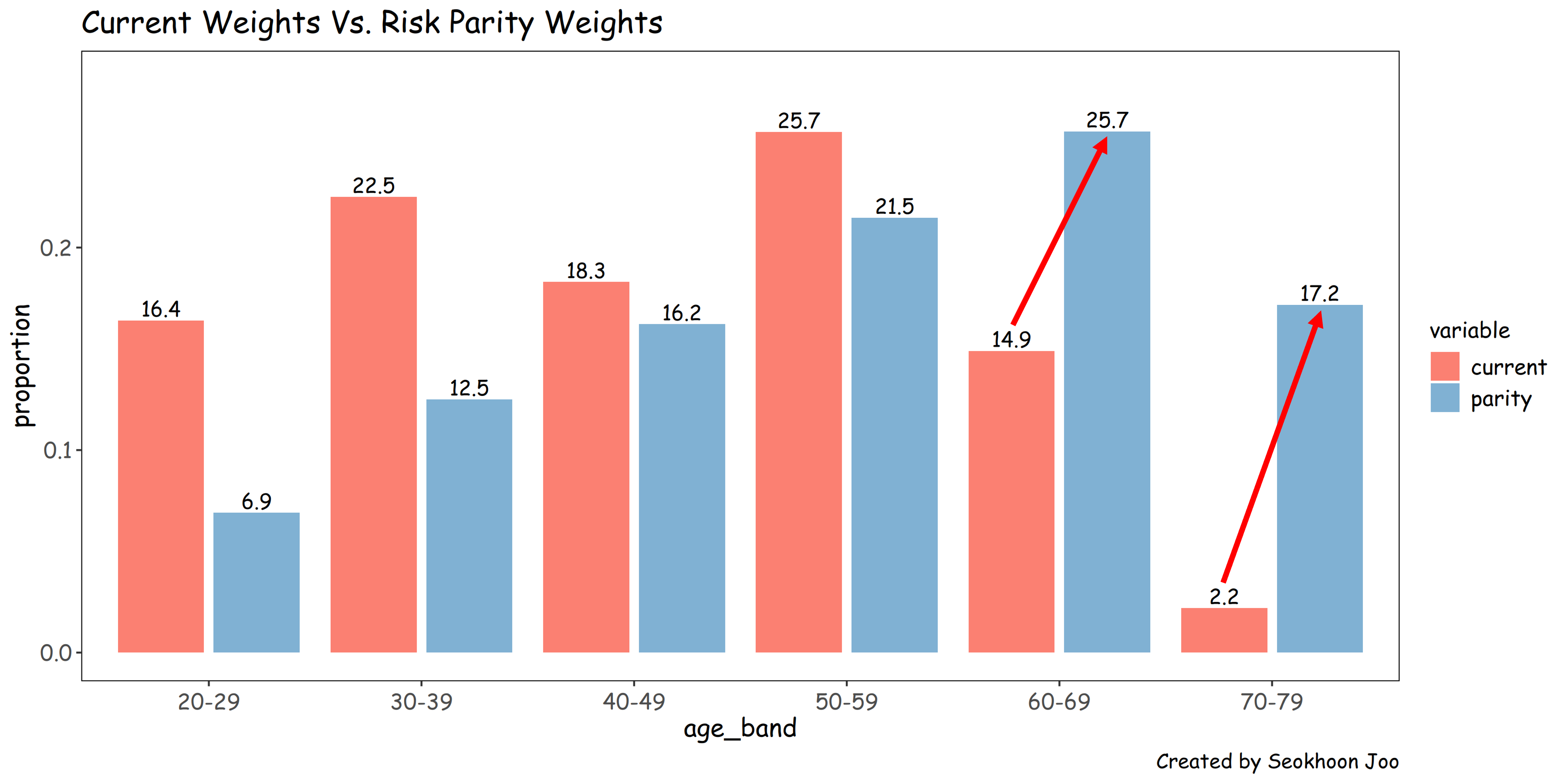
리스크 패리티를 통해 고연령 비중을 높인 새로운 판매 비중이 구해진다.
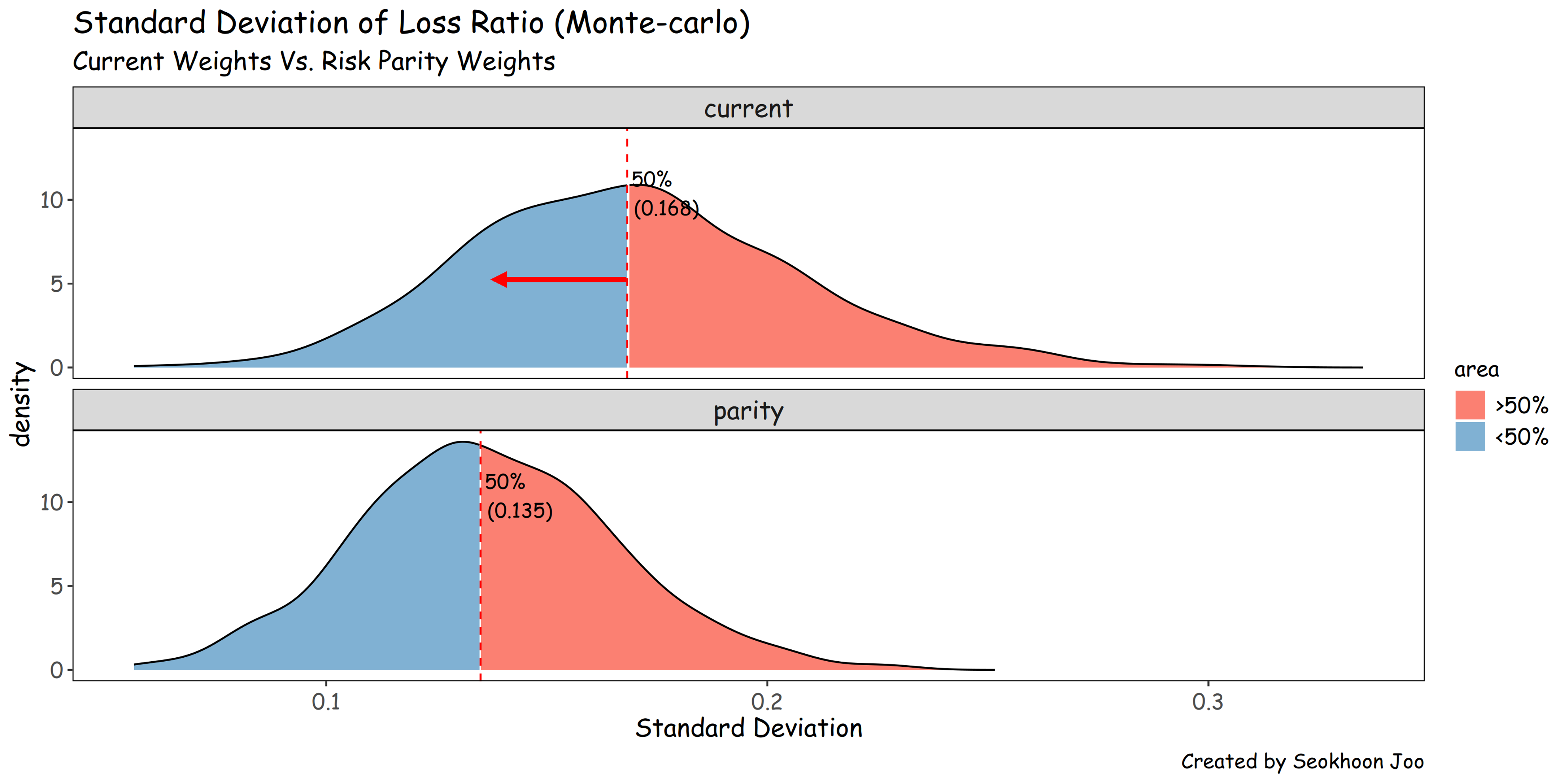
1,000번의 시뮬레이션을 통해 기존 비중의 25회차 누적 손해율(연령 합산)의 표준편차와 리스크 패리티를 적용한 표준편차의 범위를 계산해보면, 16.8에서 13.5로 낮아지는 것을 알 수 있다.
같은 방식으로 계산된 손해율의 범위는 상당한 수준으로 낮아지는데 이는 연령에 따른 손해율 차이가 뚜렷하기 때문이다.
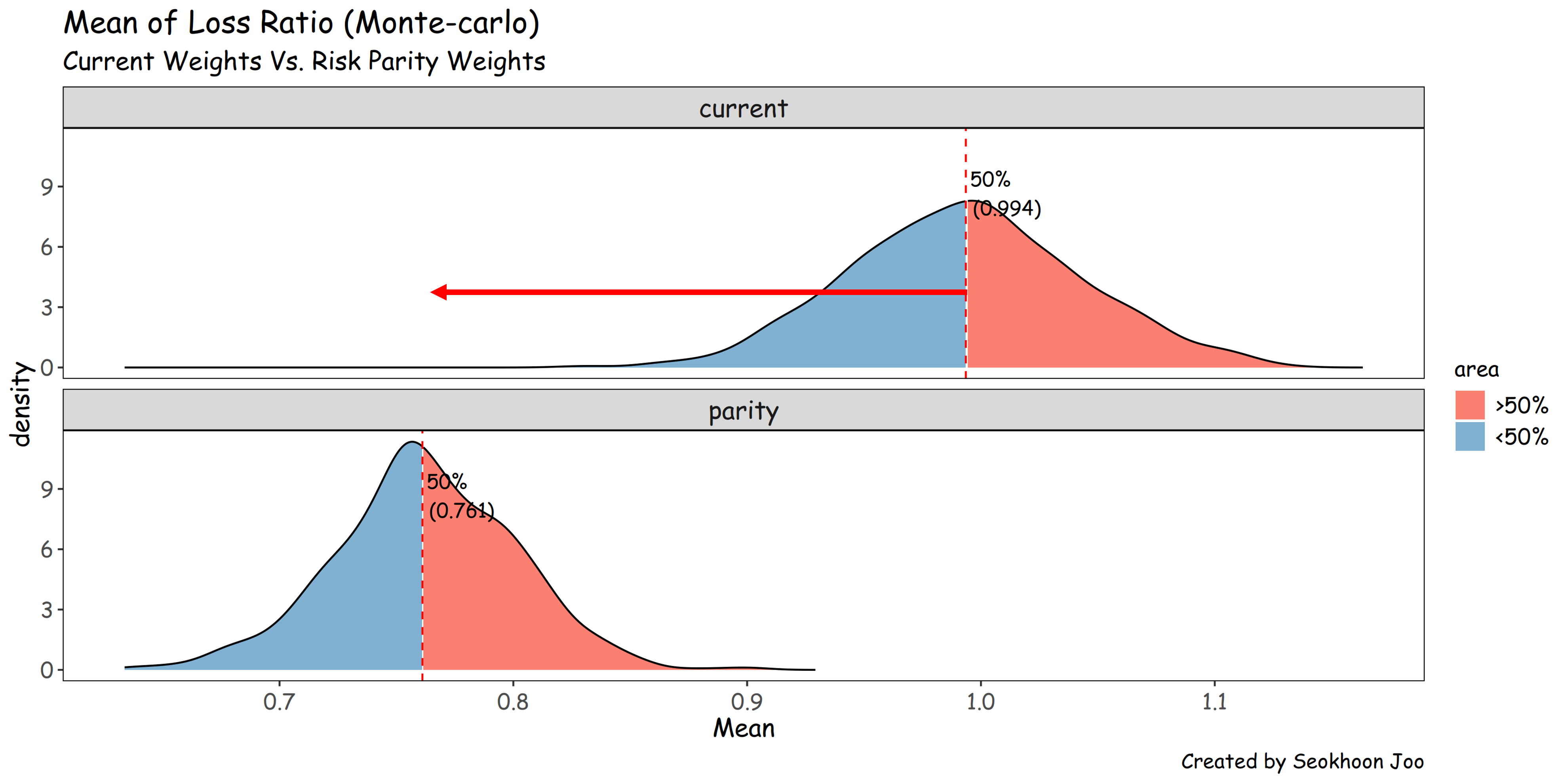
참고로 Simulation의 결과치 각 1,000개와 평균, 표준편차(X표시 된 부분)는 다음과 같다.
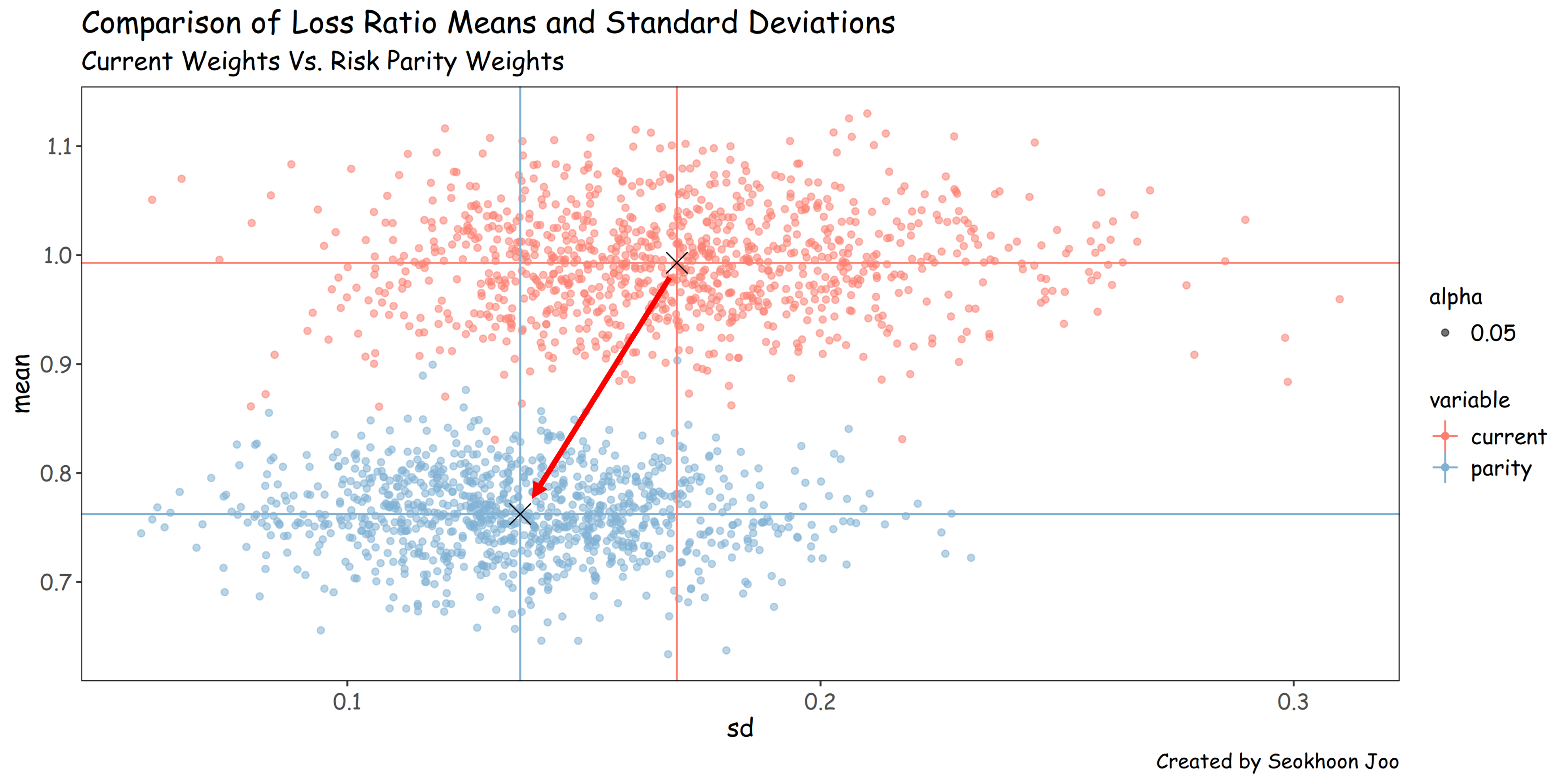
결국, 손해율에 포커스를 두고 목표 비중을 설정하지 않고, 변동성에 기반을 두고 해를 구하면 자연스럽게 손해율이 줄어드는 결과가 도출된다.
이러한 목표를 달성하기 위해 고연령 판매 비중을 확대하기 위해 해당 연령에 대한 판매 수수료를 올리는 것도 하나의 방법이 될 수 있을 것이다. (혹은 적절한 한도 확대도 가능)
5. 마치며
- 이러한 방법이 모든 상황에서 아름다운 결과를 내주지는 않는다. 담보, 한도 등 모든 것을 다 고려하다보면 복잡성이 매우 높아지고 세분화의 과정에서 필연적으로 과적합(overfitting)이 발생하기 때문이다.
- 똑같은 프로세스에 모델만 최신으로 바꾸는 것은 보험업 데이터가 새로워지거나 이전에 경험하지 못했던 통섭적 사고를 보여주지 않는 한 큰 차이를 발생시키기 어려울 것이다. 최선의 방법은 아니지만 이렇게 관점을 달리하는 것도 가끔은 필요하지 않을까.
* 정확히 틀리는 것보다 대충 맞는 게 더 낫다 - 존 메이너드 케인즈