Basic, Mack’s and Bootstrap Chain Ladder
0. 들어가며
Chain Ladder Methods는 손실 준비금 예측의 가장 기본적인 벙법으로, 과거의 클레임 발전 패턴을 바탕으로 미래 클레임을 예측합니다. Accident Year와 Deveolopment Year 데이터를 사용하여 LDF(Loss Development Factor)를 추정하게 되는데 계산이 아주 간단하고, 데이터 난이도가 비교적 낮습니다. 과거 패턴에 의존하기 때문에 데이터 변동성이나 이상치에 민감하지 않지만, 비정상적인 데이터에 대해서는 정확도가 떨어질 가능성이 있습니다. 여기서는 총 손실 준비금과 IBNR을 중심에 두지 않고, 손해액 그 자체를 추정하는데 내용을 할애하도록 하겠습니다. 손해보험의 실무적 관점이 아니라 손해액을 추정하는 논리적 관점을 이해해주시면 감사하겠습니다. 논리적 관점을 이해하면 스스로 손해액 추정 코드를 작성할 수 있고, 다양한 변형이 가능하게 됩니다. 저도 직접 작성한 코드의 결과를 그래프로 설명 드리도록 하겠습니다.
1. Basic Chain Ladder
다음은 미국 재보험 협회의 간단한 데이터(10x10 행렬) 예시입니다
dev
origin 1 2 3 4 5 6 7 8 9 10
1981 5012 8269 10907 11805 13539 16181 18009 18608 18662 18834
1982 106 4285 5396 10666 13782 15599 15496 16169 16704 NA
1983 3410 8992 13873 16141 18735 22214 22863 23466 NA NA
1984 5655 11555 15766 21266 23425 26083 27067 NA NA NA
1985 1092 9565 15836 22169 25955 26180 NA NA NA NA
1986 1513 6445 11702 12935 15852 NA NA NA NA NA
1987 557 4020 10946 12314 NA NA NA NA NA NA
1988 1351 6947 13112 NA NA NA NA NA NA NA
1989 3133 5395 NA NA NA NA NA NA NA NA
1990 2063 NA NA NA NA NA NA NA NA NA미국 재보험 협회 데이터는 Loss triangle로 구성됩니다. 이 삼각형은 Accident Year(origin)와 Development Year(dev)로 이루어진 행렬로 각 셀에는 특정 Accident Year에 발생한 클레임의 Development 상태가 기록되어 있습니다
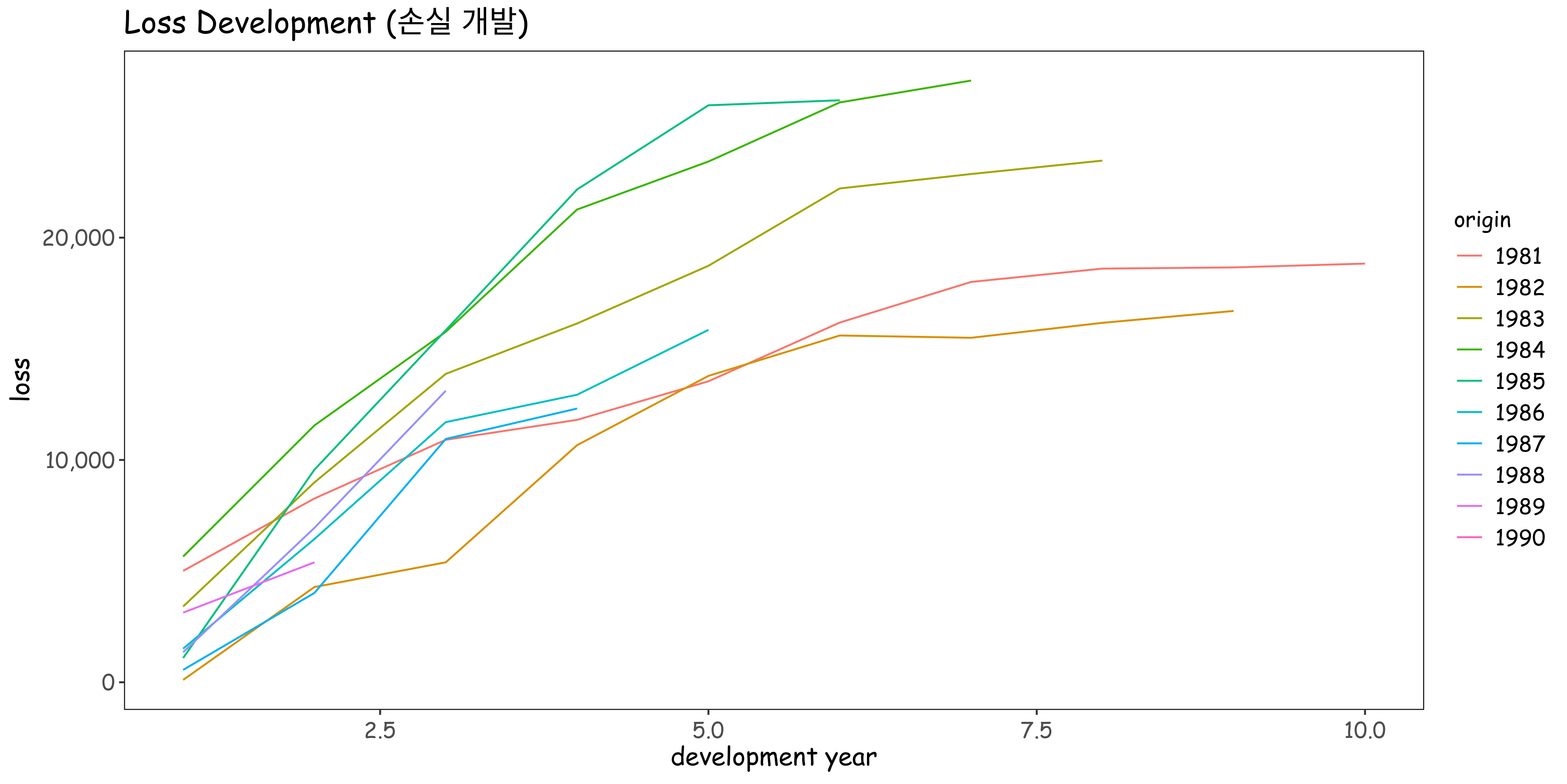
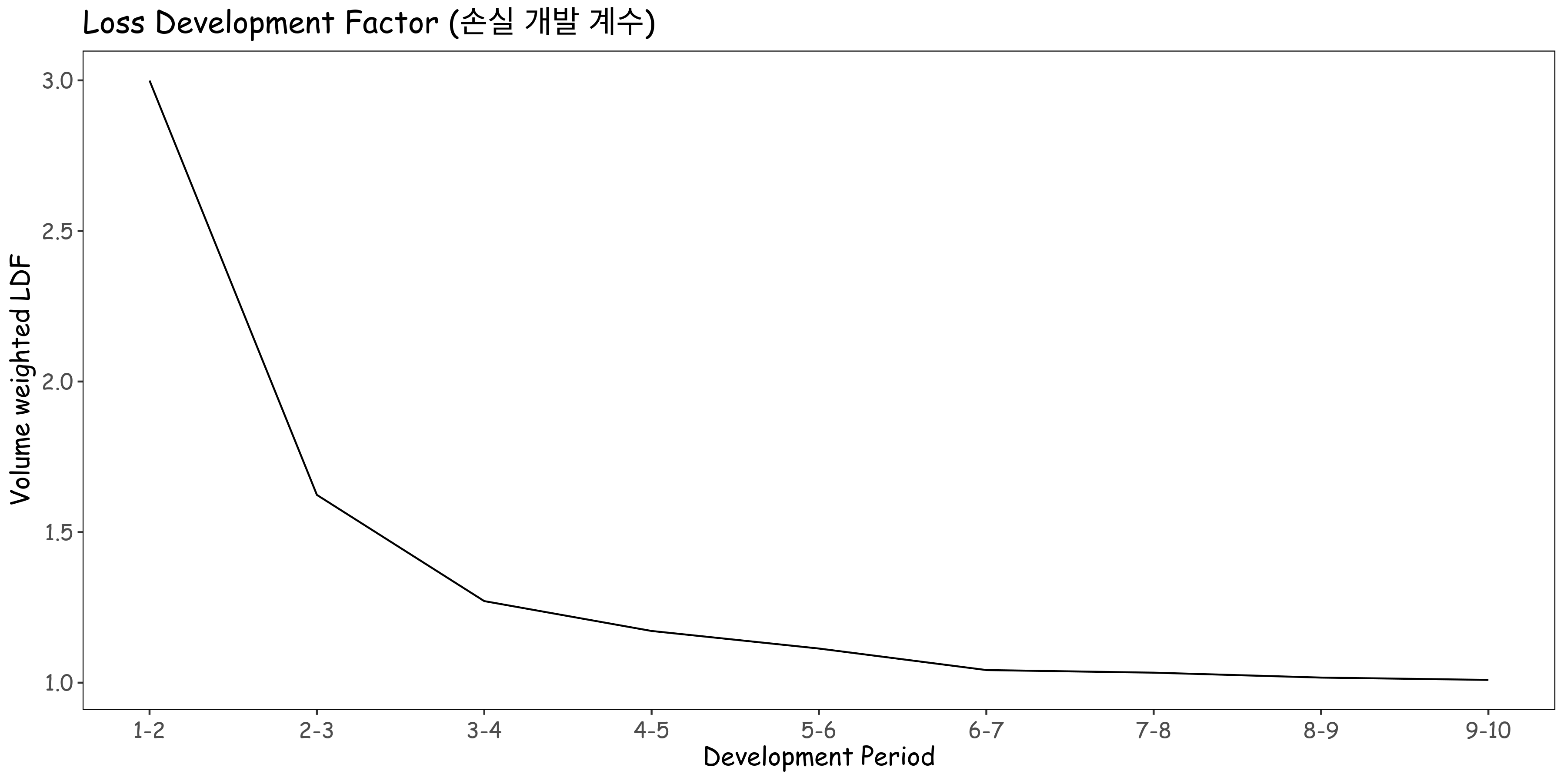
LDF는 한 개발 기간에서 다음 개발 기간까지의 Loss triangle 의 Volume weighted 평균 개발 비율로 계산됩니다.
- LDF: \(f_j = \frac{\sum_{i=1}^{n-j} C_{i, j+1}}{\sum_{i=1}^{n-j} C_{i, j}}\)
- Expected Loss: \(\hat{C}{i, n} = C{i, k_i} \times \prod_{j=k_i}^{n-1} f_j\)
다만, 여기서 가장 오래된 1981의 10번째 손실 개발 계수를 최종으로 가정하는 것이 적합하지 않을 수 있습니다. 로그 선형 모델을 가정하고 산점도를 그려보면 다음과 같습니다. (다양한 방법이 있습니다.)
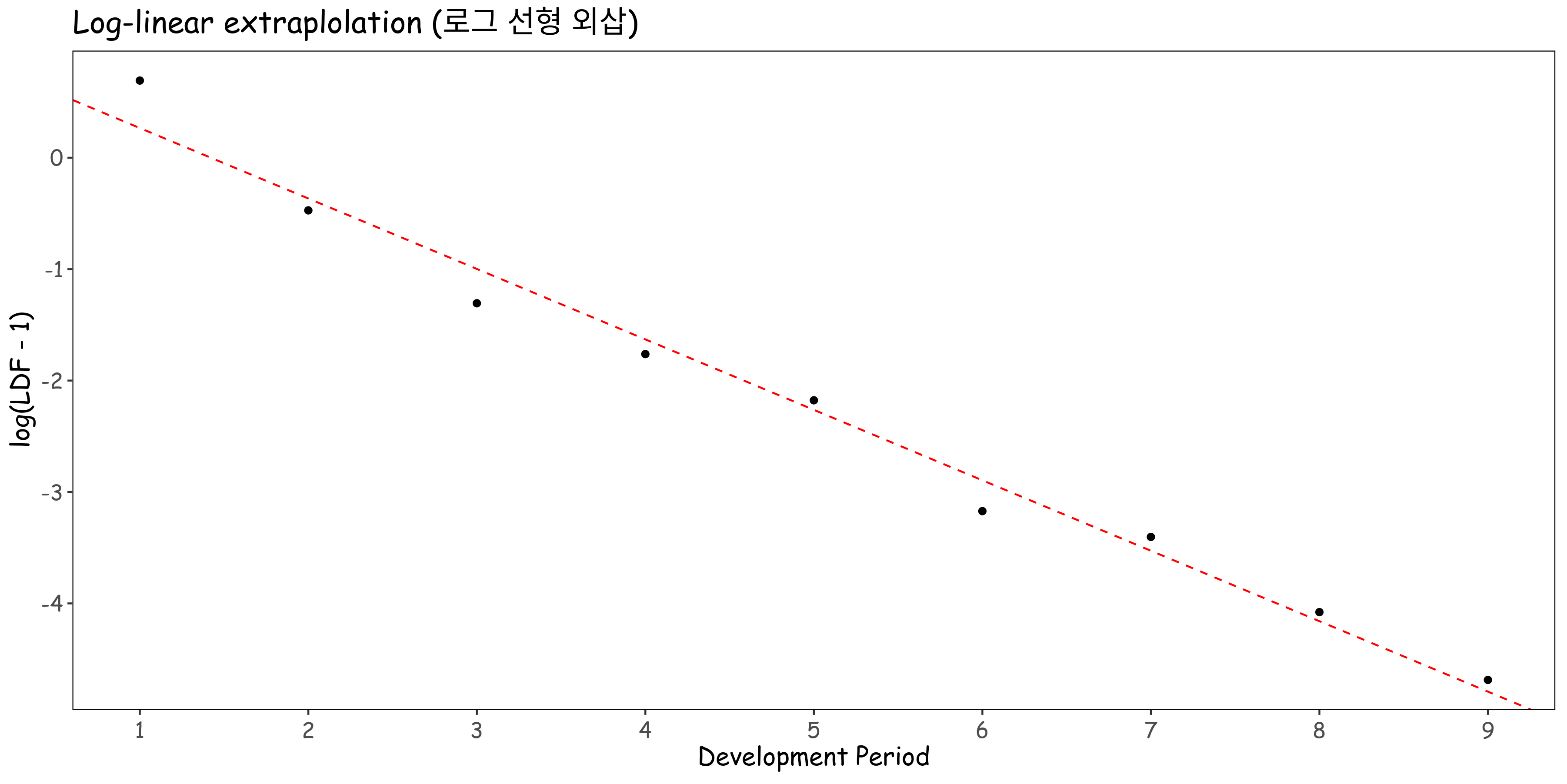
외삽이 잘 적용된다는 것을 알 수 있고, 수렴 기준을 정하기 위해 \(\epsilon = 0.0001\)로 설정하면 15회차를 최종으로 가정하게 됩니다. 이를 토대로 아래와 같은 Ulitmate Loss로 수렴하는 예상 손실 개발 패턴을 확인할 수 있습니다.
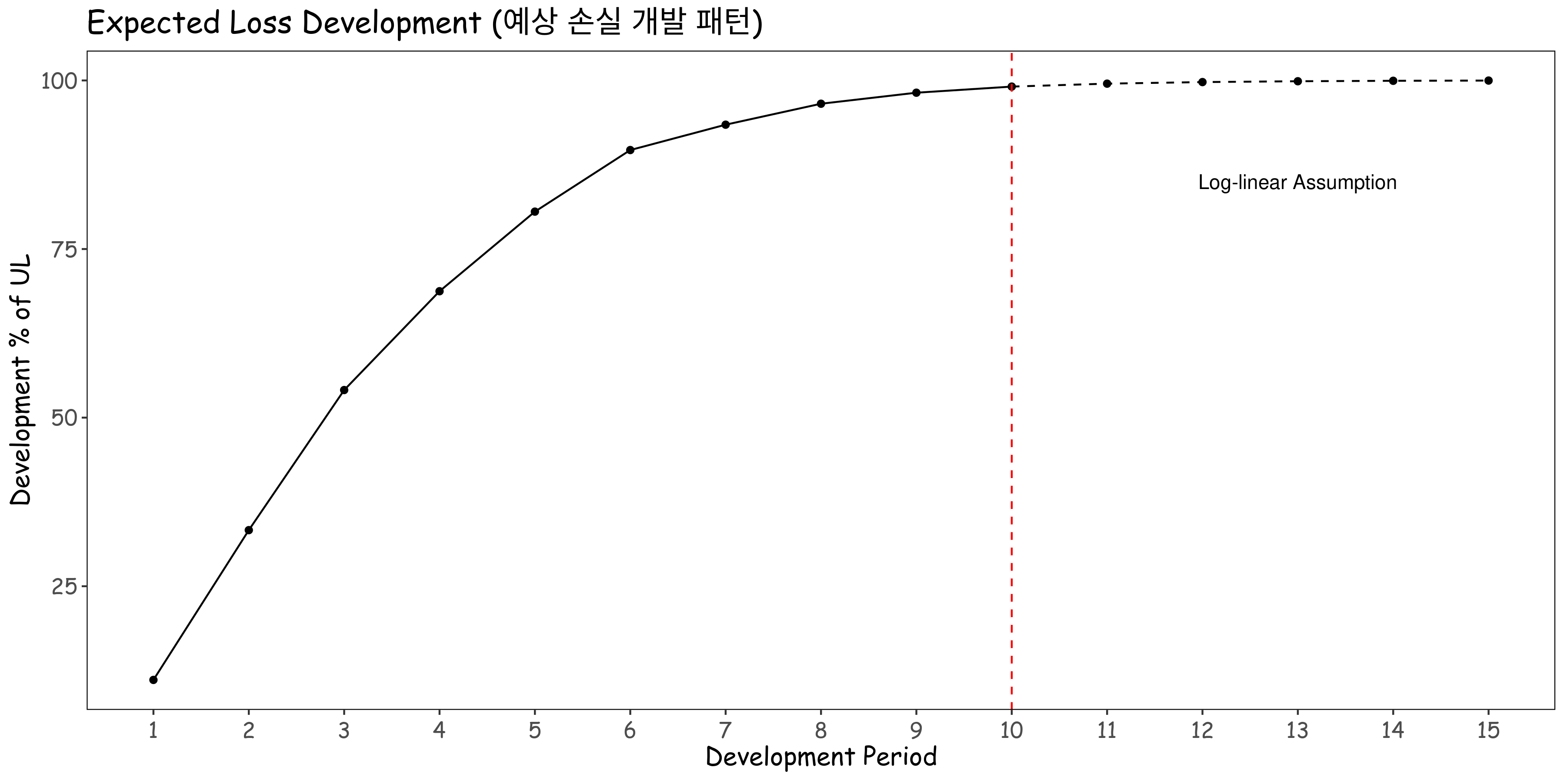
이런 방식으로 예상 손해액을 추정하면 다음과 같습니다.
dev
origin 1 2 3 4 5 6 7 8 9 10
1981 5012 8269 10907 11805 13539 16181 18009 18608 18662 18834
1982 106 4285 5396 10666 13782 15599 15496 16169 16704 16858
1983 3410 8992 13873 16141 18735 22214 22863 23466 23863 24083
1984 5655 11555 15766 21266 23425 26083 27067 27967 28441 28703
1985 1092 9565 15836 22169 25955 26180 27278 28185 28663 28927
1986 1513 6445 11702 12935 15852 17649 18389 19001 19323 19501
1987 557 4020 10946 12314 14428 16064 16738 17294 17587 17749
1988 1351 6947 13112 16664 19525 21738 22650 23403 23800 24019
1989 3133 5395 8759 11132 13043 14521 15130 15634 15898 16045
1990 2063 6188 10046 12767 14959 16655 17353 17931 18234 18402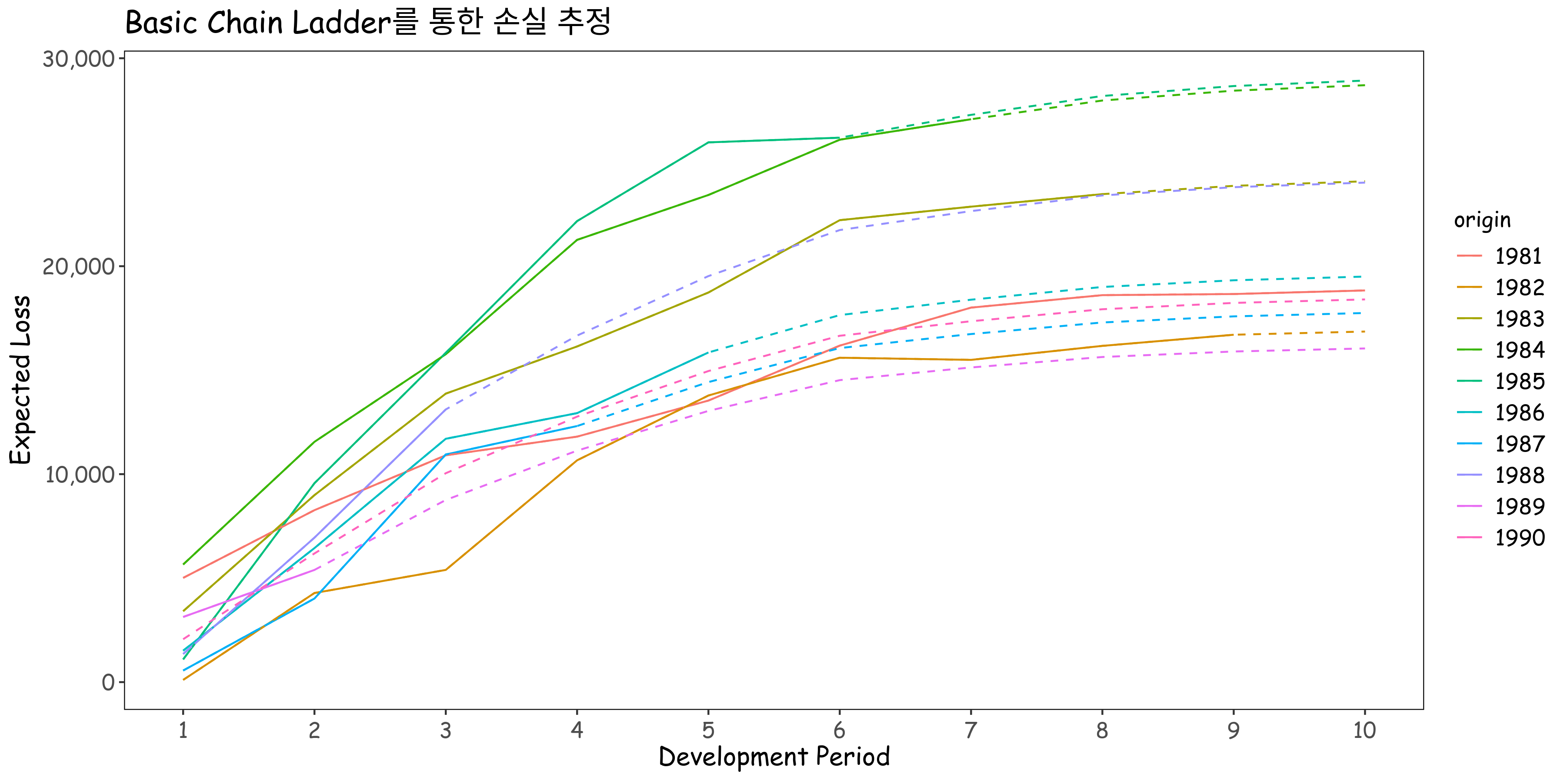
손실 준비금의 형태는 다음과 같습니다. 예상 Ultimate Loss에서 최근까지의 Loss를 제외한 부분을 IBNR이라고 추정할 수 있습니다.
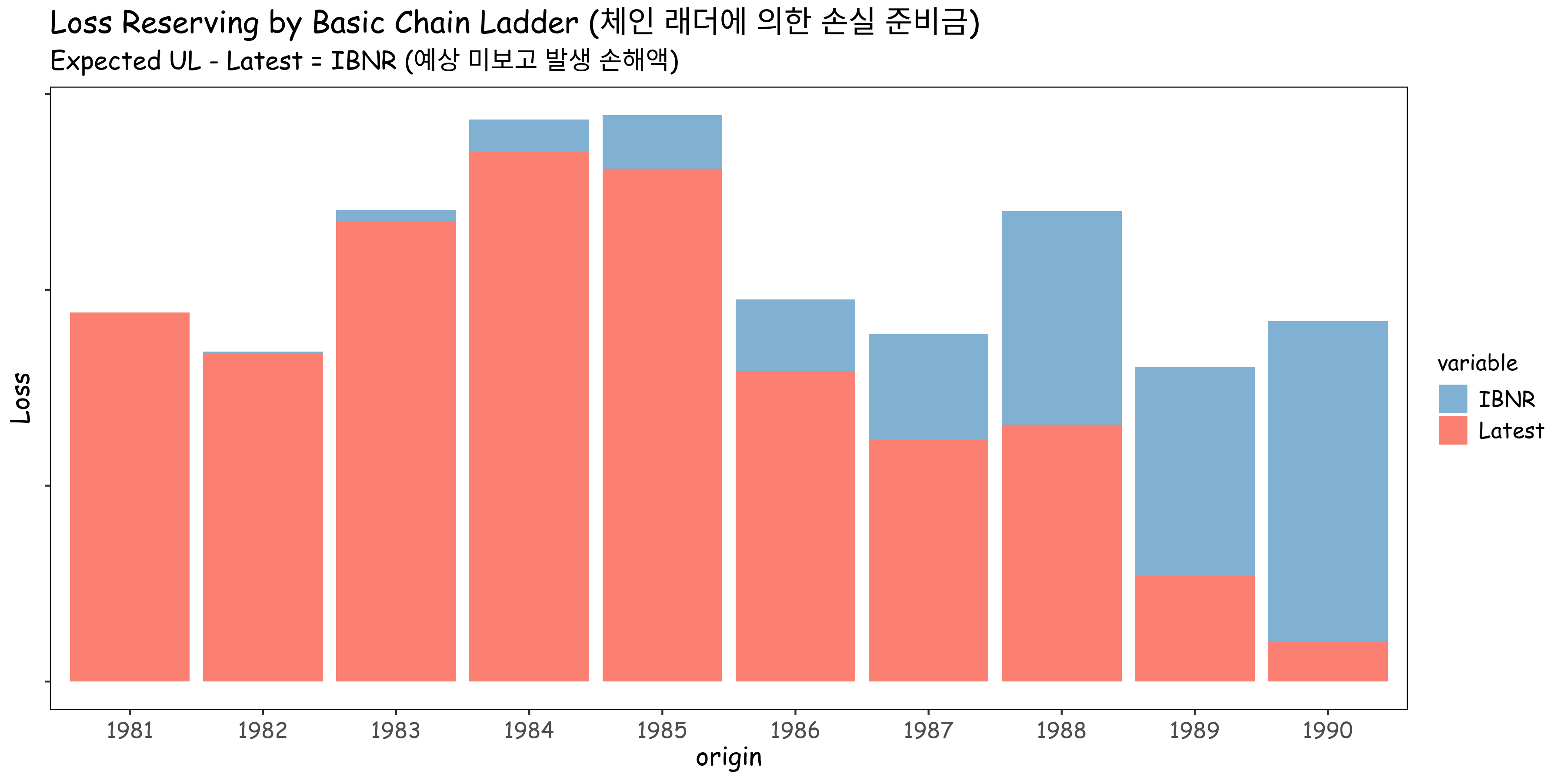
2. Mack’s Chain Ladder
Mack’s Chain Ladder는 Chain Ladder의 확률론적(Stochastic) 확장으로, 손실 준비금의 평균 추정치와 함께 그 변동성을 평가합니다. 여기서는 LDF를 원점을 통과하는 선형회귀 모델의 계수로 설정합니다. 만약 10개의 Development Year가 있다면, 9개의 선형회귀 모델이 구성되고 각각의 회귀계수가 계산됩니다. Mack의 분산은 Process Risk와 Parameter Risk의 합으로 구할 수 있는데 이 모든 것들이 LDF의 분산으로 부터 계산됩니다.
- LDF의 분산: \(\text{Var}(f_j) = \frac{1}{n - j} \sum_{i=1}^{n-j} \left( \frac{C_{i, j+1}}{C_{i, j}} - f_j \right)^2\)
- 총 준비금 추정 표준오차: \(\text{SE}(\hat{R}) = \sqrt{\sum_{j=1}^{n-1} \left( \sum_{i=n-j+1}^{n} C_{i, j} \cdot \prod_{k=j}^{n-1} f_k \right)^2 \cdot \text{Var}(f_j)}\)
LDF의 선형회귀 모델로부터 계산된 표준화 잔차와 각 변수간의 무작위성을 확인해 봅시다. 빨간 선은 Lowess (Locally Weighted Scatterplot Smoothing) 알고리즘에 의해 그려진 (비선형성을 보기 위한) 회귀 선입니다. fitted value와 표준화 잔차간의 트렌드가 보이는 듯 하나 신경쓸 정도는 아닙니다.
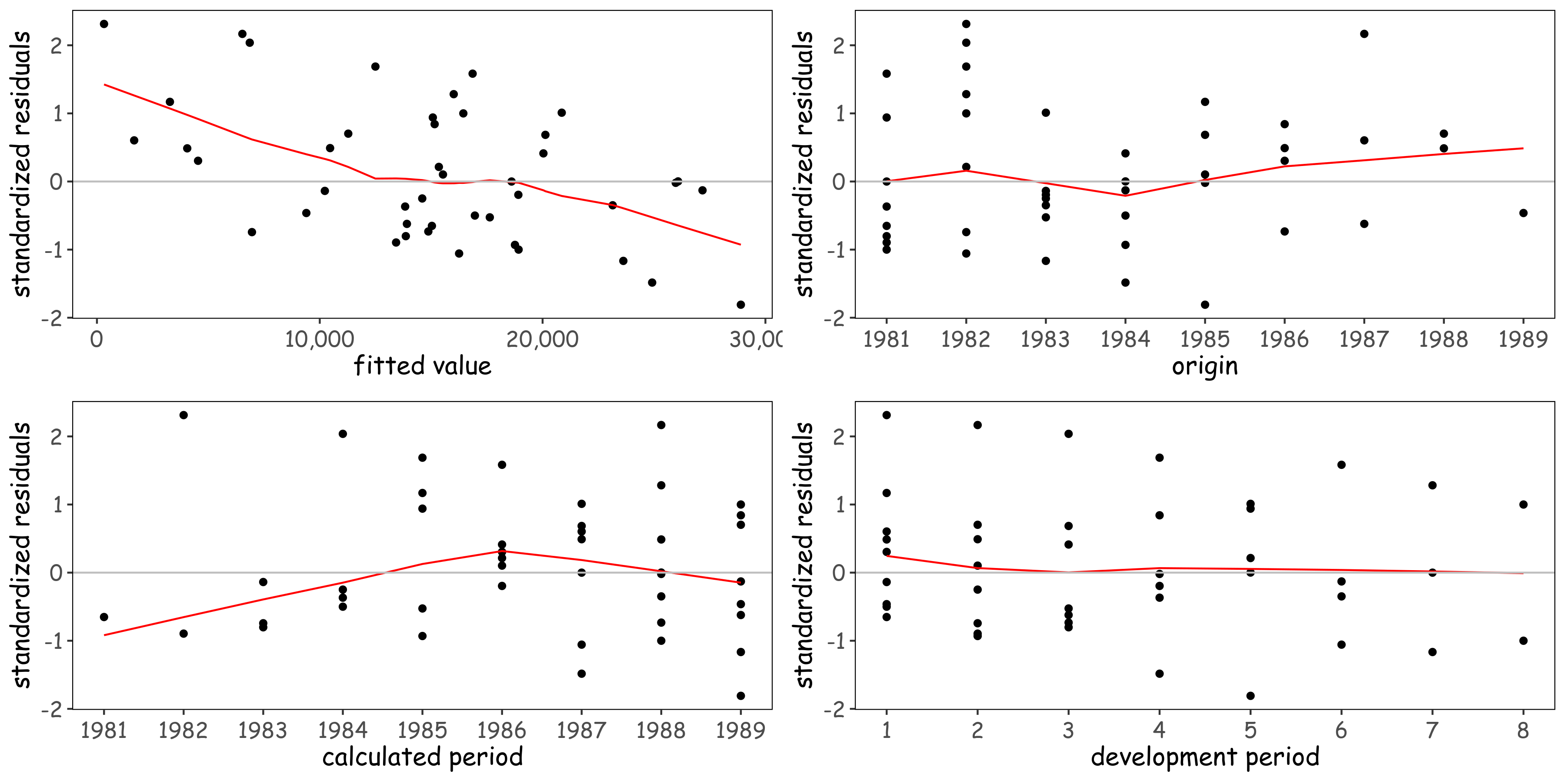
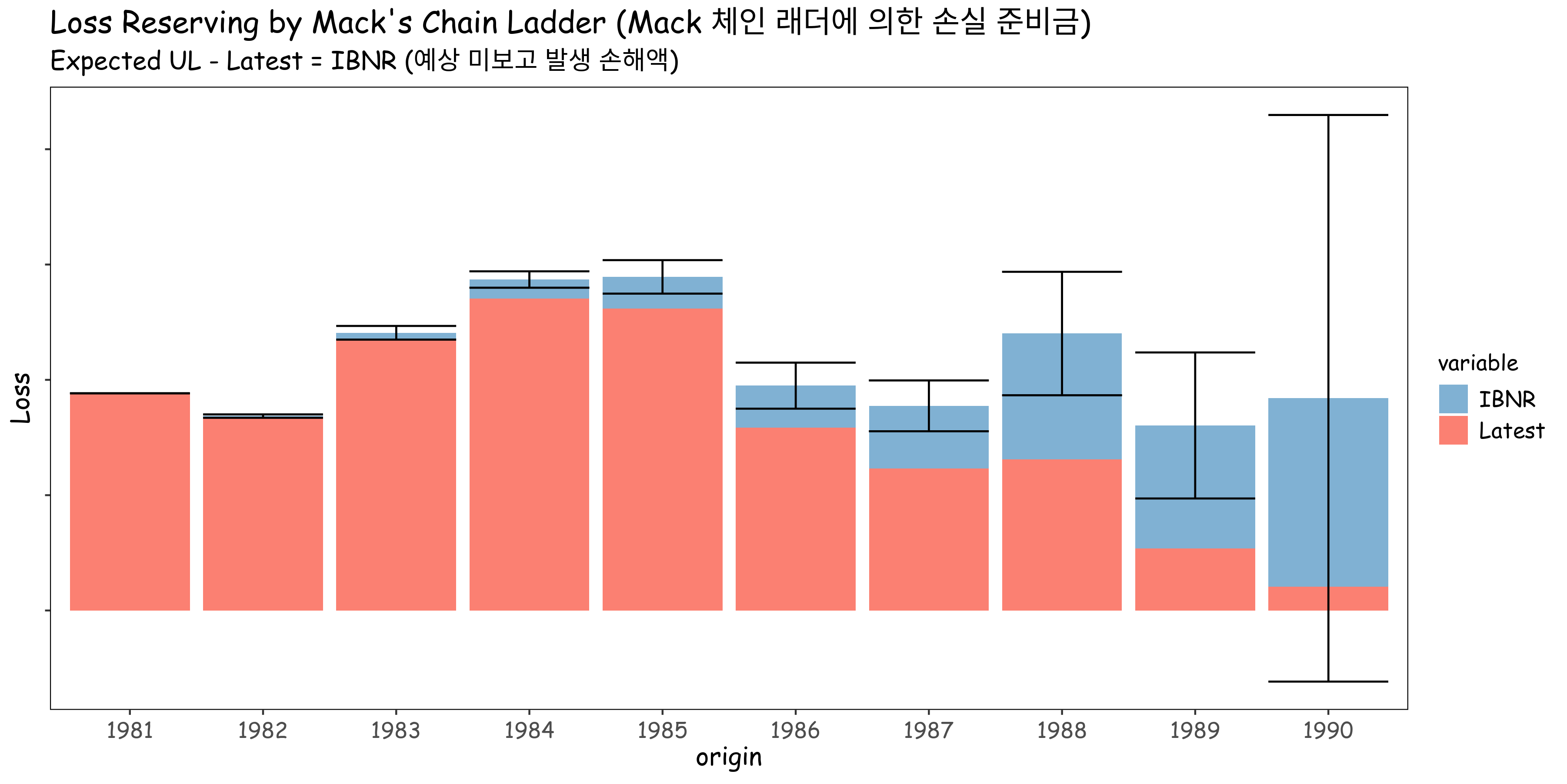
예상 손해액과 표준오차를 표현하면 다음과 같습니다. 짧은 Development Period를 가지고 있을수록 예측해야 하는 기간이 길어지므로 오차가 커집니다.
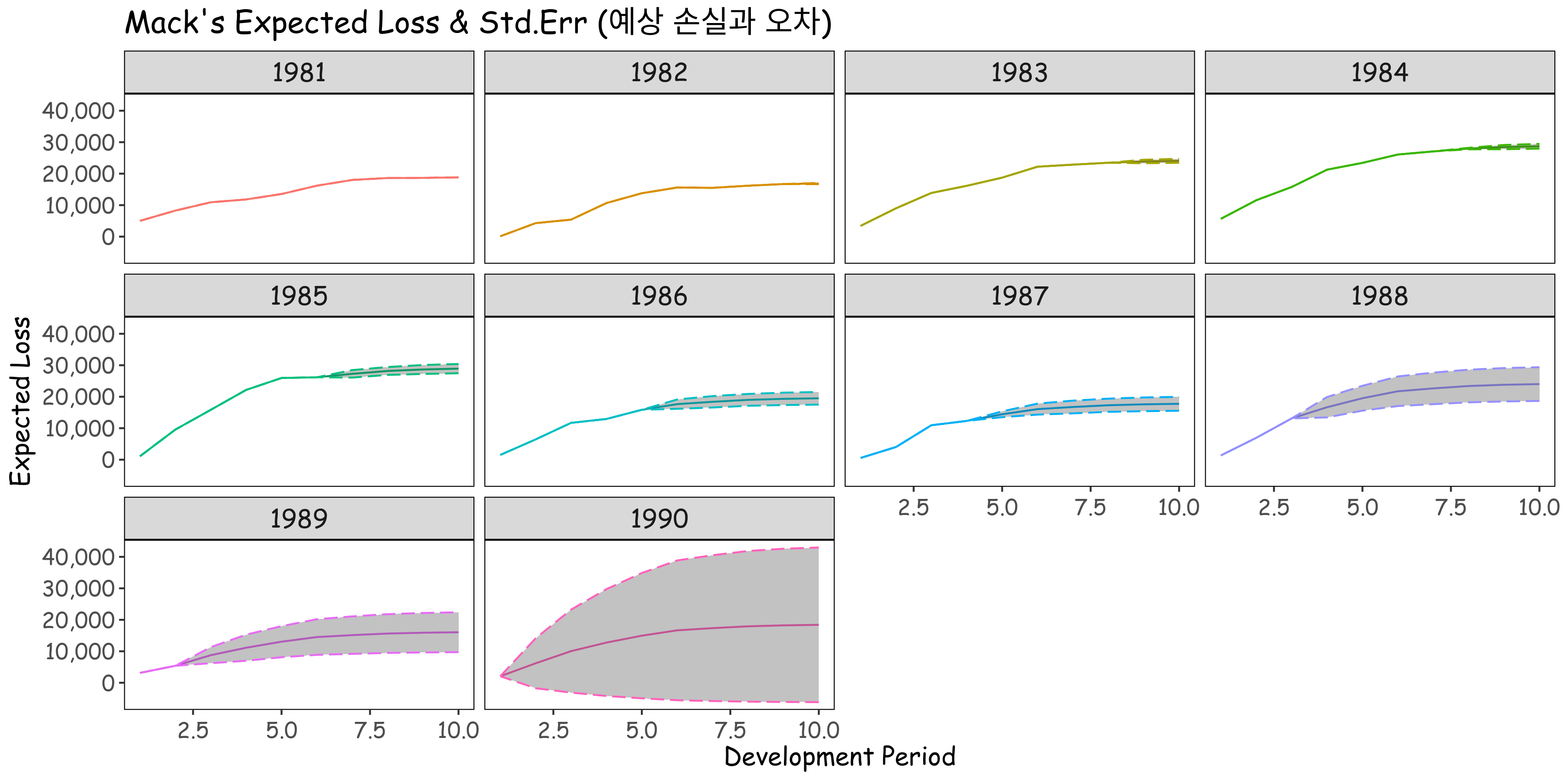
손실 준비금의 형태는 Basic Chain Ladder와 같습니다. 다만 추가로 손실 준비금의 오차 범위를 알 수 있게 됩니다. Mack의 방법은 Chain Ladder에 변동성을 추가함으로써 구간 추정을 할 수 있다는데 큰 의미가 있습니다.
3. Bootstrap Chain Ladder
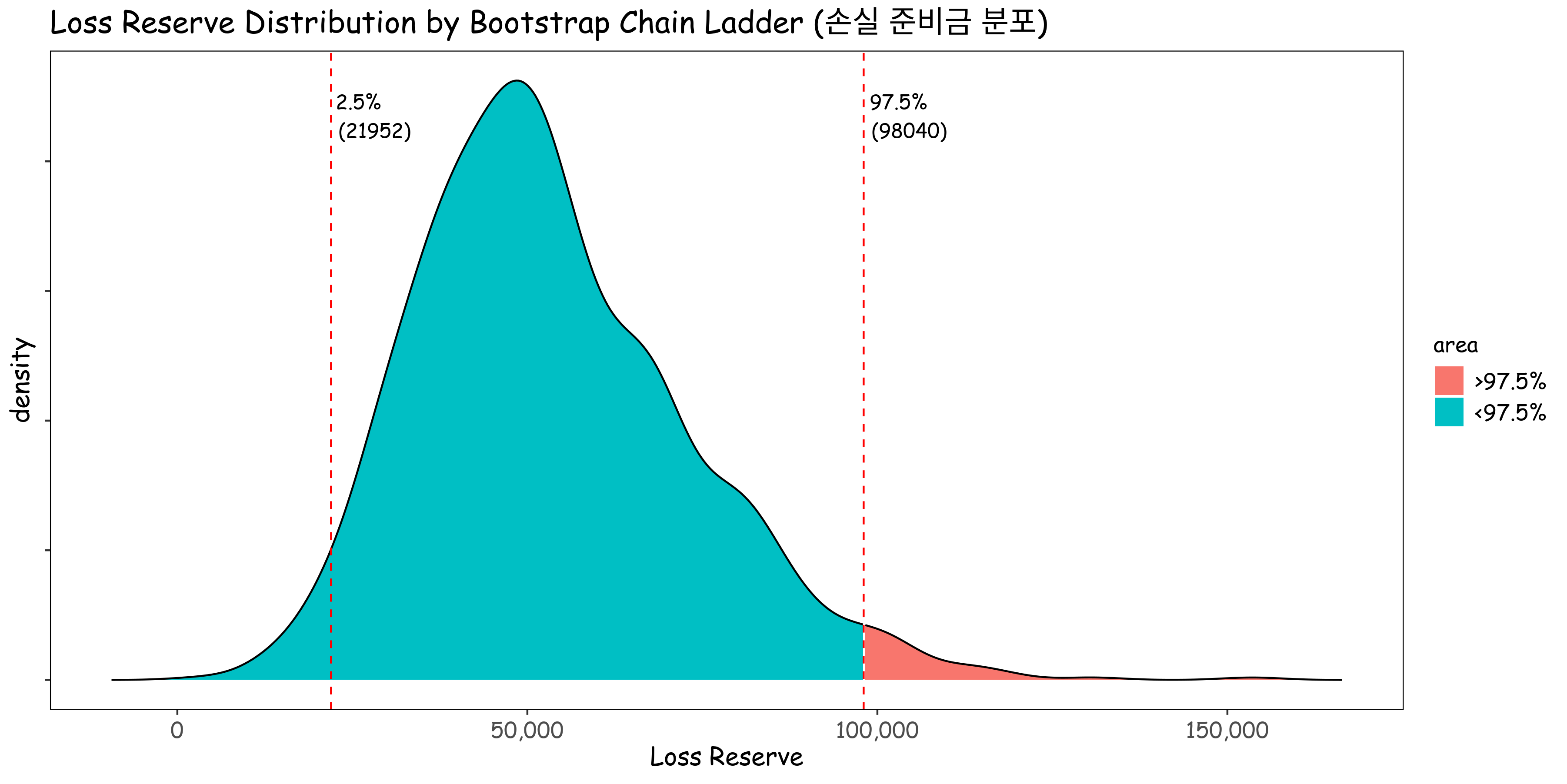
Bootstrap Chain Ladder도 LDF를 구하는 과정은 같습니다. 다만 예상 손해액과 실제 손해액의 차이를 이용해 잔차를 구하고 이 잔차를 리샘플링하여 다양한 가상 Loss triangle을 생성한 후, 이로부터 손실 준비금 추정치 분포를 계산하는 것입니다. 다음은 1,000번의 리샘플링을 통해 계산된 예상 손실 준비금 분포입니다. 컴퓨팅 파워를 이용해서 쉽게 구할 수 있습니다. 이 글을 쓰는 목적이 손실 준비금 추정이 아니기에 자세한 설명은 하지 않겠지만, 부트스트랩 방법은 정말 다양한 곳에 적용될 수 있습니다.
4. 마치며
Chain Ladder Methods는 손해액이나 손실 준비금을 추정할 때 여전히 가장 많이 쓰이고 있는 방법입니다. 최근 Loss Triangle이 아닌 Raw Data를 활용해 Machine Learning (GLM, xgboost, random forest, extra-tree)을 이용한 방법, 최근에는 Deep Learning을 이용한 deep triangle (2019), generalized deep triangle (2023) 등 다양한 방법들이 등장하게 되었습니다. 이 모델들은 복잡한 데이터 구조를 처리할 수 있고 다양한 입력 변수를 통합할 수 있지만, 여전히 과적합의 위험이 있고 해석이 어렵다는 단점이 있습니다 (저도 데이터가 충분하고 안정적일 때만 사용합니다). 그런 측면에서 보면 여전히 Chain Ladder Methods는 적은 데이터를 요구하면서도 다양한 커스터마이징이 가능한 효율적인 방법이라는 생각입니다. 여기서 소개하지는 않았지만 저같은 경우도 Chain Ladder 논문에는 존재하지 않는 장기상품의 손해율을 구할 때 월별 데이터의 적합, 예측 가능 임계점의 계산 등에 활용하고 있습니다. 그리고 이러한 내용을 가상 언더라이팅의 손해율 예측에도 적용하고 있습니다. 기회가 된다면, 다음에는 Machine Learning 방법과 Deep Learning 방법에 대해서 소개하도록 하겠습니다. 감사합니다.